فیبوناچی چیست؟
به گزارش «تابناک»، لئوناردو فیبوناچی (Leonardo de pisa de Fibonacci) ریاضیدان برجسته اروپایی در قرن یازدهم میلادی زندگی میکرد. فیبوناچی اولین فردی بود که اعداد هندی-عربی (…، ۱،۲،۳،۴،۵) را به اروپا معرفی کرد. یکی از مهمترین اقدامات او معرفی سری معروف فیبوناچی است. در این سری که با صفر و یک شروع میشود، هر عدد از مجموع دو عدد قبلی به دست میآید. رابطه فیبوناچی به شکل زیر است:

در صورت پیروی از قواعد مذکور به دنباله زیر خواهیم رسید:
… ، ۲۳۳ ، ۱۴۴ ، ۸۹ ، ۵۵ ، ۳۴ ، ۲۱ ، ۱۳ ، ۸ ، ۵ ، ۳ ، ۲ ، ۱ ، ۱ ، ۰
درواقع ایده پیدایش این سری در سال ۱۲۰۲ اتفاق افتاد که فیبوناچی به مسئله عجیبی علاقهمند شد. او میخواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آنها تعریف کند، درنهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود:
شما یک جفت خرگوش نر و ماده دارید که همین الآن به دنیا آمدهاند.
خرگوشها پس از یک ماه بالغ میشوند.
دوران بارداری خرگوشها یک ماه است.
هنگامیکه خرگوش ماده به سن بلوغ میرسد، حتماً باردار میشود.
در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده به دنیا میآورد.
خرگوشها هرگز نمیمیرند.
حساب کنید پس از n ماه چند جفت از این نوع خرگوش خواهیم داشت؟
فرض کنیم xn تعداد جفت خرگوش پس از n ماه باشد.

میدانیم که x۲=۱،x۱=۱، تعداد جفت خرگوشها در ماه n+1 ام برابر خواهد بود با حاصل جمع تعداد جفت خرگوشهایی که در این ماه متولد میشوند، بهاضافه تعداد جفت خرگوش¬های موجود. (xn) اما چون هر جفت خرگوش که از دو ماه قبل موجود بوده هم، اکنون حداقل دو ماه سن خواهند داشت و به سن زادوولد رسیدهاند، تعداد جفت خرگوشهای متولدشده برابر خواهد بود با xn-۱ ، پس خواهیم داشت:
x۱ = ۱ , x۲ = ۱, xn+۱ = xn + xn-۱
فیبوناچی با حل این مسئله از راهحل فوق، دنباله حاصل را به جهان ریاضیات معرفی کرد که خواص شگفتانگیز و کاربردهای فراوان آن تا به امروز نهتنها نظر ریاضیدانان، بلکه دانشمندان بسیاری از رشتههای دیگر را به خود جلب کرده است.
وجود سری فیبوناچی در طبیعت
وجود نظم در اجزای مختلف طبیعت قابلمشاهده است. ریاضیات یکی از علوم پایهای است که به کمک آن میتوان به بسیاری از نظمهای موجود در طبیعت پی برد. اعداد فیبوناچی یکی از این نظمها است.
یکی دیگر از دلایل مشهور شدن سری فیبوناچی، این است که خارجقسمت هر دو جمله کنار هم به عدد تقریبی ۱.۶۱۸، نسبت طلایی یا عدد فی، میرسد.
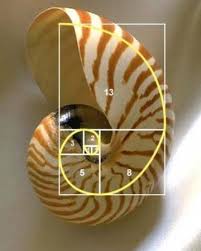
در قسمت لاک حلزون از عدد فی استفاده شده است. شاخ و برگ درختان بهصورت تصادفی در جهات مختلف رشد نمیکنند. اندازهگیری زاویه شاخهها نشان میدهد که در الگوی رشد آنها، نظمی شبیه دنباله فیبوناچی و نسبت طلایی وجود دارد. درختان با پیروی از این نوع الگوی رشد، قادر هستند درصد بیشتری از نور خورشید را جذب کنند. دانههای آفتابگردان نیز به شکل مارپیچهایی روبروی هم رشد میکنند. طبق تحقیقات انجامشده، نسبت قطر هر مارپیچ به مارپیچ بعدی ۱.۶۱۸ است. حتی در ساختار گوش ما هم از این عدد تبعیت شده است.
بسیاری نمونه دیگر در طبیعت، آناتومی بدن انسان، سازههای بزرگ تاریخی و … وجود دارد که این سری در آنها مشاهده میشود.
ارتباط عدد طلایی با دنباله فیبوناچی
هرچه جفت اعداد فیبوناچی بزرگتر باشند، نسبت بین آنها تقریب بهتری از نسبت طلایی را نشان میدهد. در ادامه برخی از این نسبتها را مشاهده میکنید:
|
A |
B |
A/B |
B/A |
|
۲ |
۳ |
۱.۵ |
۰.۶۶۶… |
|
۳ |
۵ |
۱.۶۶۶… |
۰.۶ |
|
۵ |
۸ |
۱.۶ |
۰.۶۲۵ |
|
۸ |
۱۳ |
۱.۶۲۵ |
۰.۶۱۵۳۸ |
|
… |
… |
… |
…… |
|
۱۴۴ |
۲۳۳ |
۱.۶۱۸۰۵۵۵۵۶… |
۰.۶۱۸۰۲۵ |
|
۲۳۳ |
۳۷۷ |
۱.۶۱۸۰۲۵۷۵۱… |
۰.۶۱۸۰۳۷ |
روشهای متفاوتی برای بیان رابطه بین عدد طلایی و سری فیبوناچی وجود دارد که در اینجا به یکی از این روشها اشاره میکنیم.
بهعنوان مثال، با اعداد ۲۳۳, ۱۴۴, ۸۹, ۵۵ نسبتهای زیر قابل دستیابی است:
|
۱.۶۱۸ = ۱۴۴ ÷ ۲۳۳ |
۱.۶۱۸ = ۸۹ ÷ ۱۴۴ |
|
۰.۶۱۸ = ۲۳۳ ÷ ۱۴۴ |
۰.۶۱۸ = ۱۴۴ ÷ ۸۹ |
|
۰.۳۸۲ = ۲۳۳ ÷ ۸۹ |
۰.۳۸۲ = ۱۴۴ ÷ ۵۹ |
با جذر ۰.۶۱۸ عدد ۰.۷۸۶ به دست میآید. همچنین جذر ۱.۶۱۸، ۱.۲۷ میشود. بدین ترتیب نسبتهای زیر را میتوان به دست آورد:
|
۰.۲۴۷ = ۲۵% |
۰.۷۸۶ = ۷۹% |
|
۰.۳۸۲ = ۳۸% |
۱.۲۷ = ۱۲۷% |
|
۰.۵ = ۵۰% |
۱.۶۱۸ = ۱۶۲% |
|
۰.۶۱۸ = ۶۲% |
۲.۶۱۸ = ۲۶۲% |
این نسبتها در بسیاری از حوزهها کاربرد دارند.
کاربرد فیبوناچی در بازار سهام
در طی زمان ابزارهای فیبوناچی بسیاری برای تحلیل نمودارها و نقاط بازگشت معرفی شده است. این ابزارها نشاندهنده محدودههای حمایت و مقاومت هستند که با روشهای گوناگون رسم میگردند. این سطوح بازگشتی، مانند حمایت و مقاومتهای قبلی که فقط قیمتی خاص را نقطه حساس تلقی میکردند، نیستند و میتوانند علاوه بر قیمتی خاص، یک منحنی روی نمودار، خطی مورب یا زمان خاصی را بهعنوان نقاط حساس حمایت و مقاومت تعریف کنند.
از میان ابزارهای موجود، چند ابزار بیشترین کاربرد را دارند. فیبوناچی اصلاحی، فیبوناچی خارجی، فیبوناچی انبساطی، فیبوناچی پروژکشن، فیبوناچی اکسپنشن و … از مواردی هستند که بهوسیله آنها میتوان روند قیمت سهام را پیشبینی کرد. برای کسب اطلاعات بیشتر درباره ابزارهای مختلف تحلیل تکنیکال میتوانید به مطلب «ابزارهای تحلیل تکنیکال» مراجعه کنید.



سایت تابناک از انتشار نظرات حاوی توهین و افترا و نوشته شده با حروف لاتین (فینگیلیش) معذور است.